bayesbox3

1 Setup

library(tidyverse)
library(ggpubr)

2 Aufgabe

Sie führen ein zweiwertiges (binomiales) Zufallsexperiment $n$-mal durch, dabei erzielen Sie $k$ Treffer. Die Wiederholungen sind unabhängig voneinander, und die Trefferwahrscheinlichkeit $\pi$ bleibt konstant.

(Eine Münze wiederholt werfen wäre das typische Beispiel für ein solches Zufallexperiment.)

Gehen Sie von folgenden Parameterwerten aus:

n <- 14
k <- 7  # Trefferzahl

Welcher Parameterwert $\pi$ ist am wahrscheinlichsten, wenn Sie keine weiteren Informationen haben?

Sie überprüfen alle 11 Parameterwerte für $\pi$ von 0 bis 1 (in Schritten von 0.1.)

Um diese Frage zu beantworten, berechnen Sie die Wahrscheinlichkeiten für alle möglichen Parameterwerte $\pi$ von 0 bis 1 in Schritten von 0.1 anhand einer Bayesbox. Dabei gehen wir von einer Binomialverteilung aus:

$k\sim Bin(n,\pi )$.

Listing 1: Parameterwerte (Gitter) für Trefferwahrscheinlichkeit: 0, 0.1, 0.2, …, 1

pis <- seq(from = 0, to = 1, by = 0.1)  # Parameterwerte
pis

 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Dann berechnen wir schon mal die Wahrscheinlichkeit der Daten gegeben jeweils eines Parameterwerts:

Likelihood <- dbinom(k, size = n, prob = pis)
Likelihood

 [1] 0.0000000000 0.0001641515 0.0092127048 0.0618133587 0.1574076993
 [6] 0.2094726563 0.1574076993 0.0618133587 0.0092127048 0.0001641515
[11] 0.0000000000

Auf dieser Basis erstellen wir eine Bayes-Box, um die Posteriori-Wahrscheinlichkeiten für alle Parameterwerte zu berechnen, s. Listing 2.

Listing 2: Wir basteln uns eine Bayes-Box

d <-
  tibble(
    # definiere die Hypothesen (die Parameterwerte, p): 
    p = pis,
    # Lege den Priori-Wert fest:
    Priori  = 1/11) |> 
    mutate(
      # berechne Likelihood für jeden Wasseranteil (Parameterwert):
      Likelihood = Likelihood,
      # berechne unstand. Posteriori-Werte:
      unstd_Post = Likelihood * Priori,
      # berechne Evidenz, d.i. die Summe aller unstand. Post-Werte:
      Evidenz = sum(unstd_Post),
      # berechne stand. Posteriori-Werte (summiert zu 1):
      Post = unstd_Post / Evidenz)  

Die Bayes-Box (Table 1) zeigt, wie sich die Post-Verteilung berechnet.

Leider sind die zentralen Spalten ausgeblendet. 🤬

Table 1: Die Bayes-Box

id	p	Priori
1	0.0	0.09
2	0.1	0.09
3	0.2	0.09
4	0.3	0.09
5	0.4	0.09
6	0.5	0.09
7	0.6	0.09
8	0.7	0.09
9	0.8	0.09
10	0.9	0.09
11	1.0	0.09

Aufgabe: Welcher Parameterwert $\pi$ ist am wahrscheinlichsten?

3 Lösung

Der wahrscheinlichste Parameterwert $\pi$ ist derjenige, der die höchste Posteriori-Wahrscheinlichkeit hat.

Bei gleichverteilten Prirori-Werten ist der wahrscheinlichste Parameterwert derjenige, der die höchste Likelihood hat: 7/14 = 0.5.

Man braucht also die Bayesbox gar nicht  🤪.

id	p	Priori	Likelihood	unstd_Post	Evidenz	Post
1	0.0	0.09	0.00	0.00	0.06	0.00
2	0.1	0.09	0.00	0.00	0.06	0.00
3	0.2	0.09	0.01	0.00	0.06	0.01
4	0.3	0.09	0.06	0.01	0.06	0.09
5	0.4	0.09	0.16	0.01	0.06	0.24
6	0.5	0.09	0.21	0.02	0.06	0.31
7	0.6	0.09	0.16	0.01	0.06	0.24
8	0.7	0.09	0.06	0.01	0.06	0.09
9	0.8	0.09	0.01	0.00	0.06	0.01
10	0.9	0.09	0.00	0.00	0.06	0.00
11	1.0	0.09	0.00	0.00	0.06	0.00

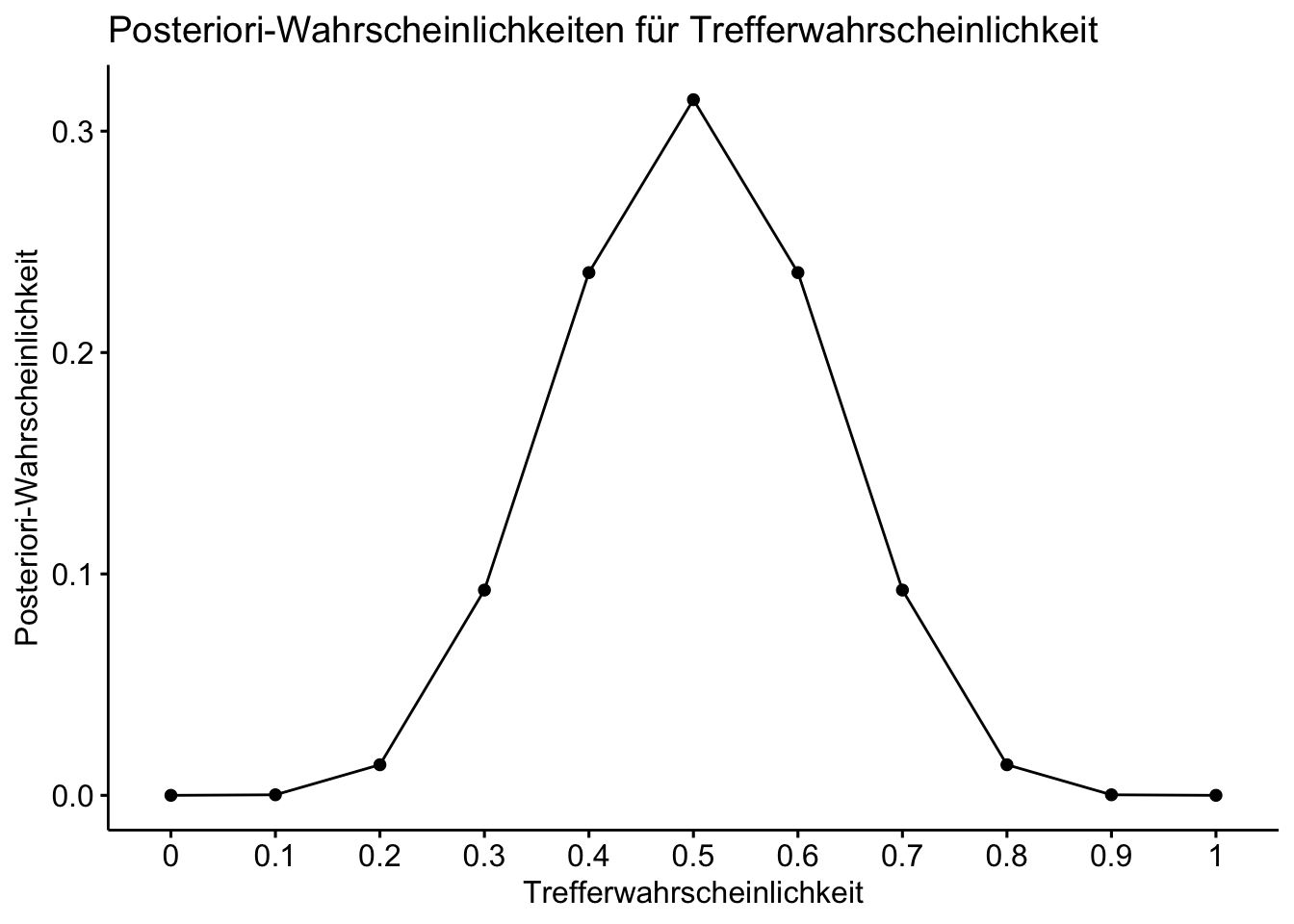
Hier ist eine Visualisierung der Posteriori-Wahrscheinlichkeiten:

ggline(d, x = "p", y = "Post", 
       xlab = "Trefferwahrscheinlichkeit", ylab = "Posteriori-Wahrscheinlichkeit",
       title = "Posteriori-Wahrscheinlichkeiten für Trefferwahrscheinlichkeit",
       add = c("point", "smooth"))