p <- .9
k <- 6
wasser_erde <- .7
wasser_bath42 <- .9
n <- 9bath42
Aufgabe
Mehrere Proben werden zu einem unbekannten Planeten geschossen. Die Forschungsfrage lautet: Ist es die Erde 0.7 oder der Planet “Bath42” mit 0.9 Wasseranteil?
Wir sind indifferent (apriori) zu den Parameterwerten.
Daten: 6 Treffer (Wasser) von 9 Versuchen (Proben).
Behauptung: “Das ist fast sicher Bath42!”.
Aufgabe: Wie groß ist die Wahrscheinlichkeit, dass es sich um Bath42 handelt (und nicht um die Erde)?
Hinweise:
- Orientieren Sie sich im Übrigen an den allgemeinen Hinweisen des Datenwerks.
Lösung
Da wir indifferent apriori sind, ist der Parameterwert mit der höchsten Likelihood am wahrscheinlichsten. Der höchsten Likelihood hat der Parameter, der gleich den Daten ist. Das ist:
k/n[1] 0.6666667Schauen wir uns die Likelihoods für alle Parameterwerte \(0, 0.1, 0.2, \ldots, 1\) an.
Hier ist eine Sequenz dieser Parameterwerte:
parameterwerte <- seq(0, 1, by = .1)
parameterwerte [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0Und hier sind die zugehörigen Likelihoods:
library(tidyverse)
likelihoods <-
tibble(
parameterwerte = parameterwerte,
likelihoods = dbinom(x = k, size = n, prob = parameterwerte))
likelihoods| parameterwerte | likelihoods |
|---|---|
| 0.0 | 0.0000000 |
| 0.1 | 0.0000612 |
| 0.2 | 0.0027525 |
| 0.3 | 0.0210039 |
| 0.4 | 0.0743178 |
| 0.5 | 0.1640625 |
| 0.6 | 0.2508227 |
| 0.7 | 0.2668279 |
| 0.8 | 0.1761608 |
| 0.9 | 0.0446410 |
| 1.0 | 0.0000000 |
Wie man sieht, hat der Parameterwert, der den Daten am nächsten kommt, die höchste Likelihood.
Die Post-Wahrscheinlichkeit können in gewohnter Manier mit Bayes’ Theorem berechnen. Vielleicht am einfachsten mit der Bayes-Box.
Eine Funktion, die die Bayes-Box berechnet, kann man sich so importieren:
# devtools::install_github("https://github.com/sebastiansauer/prada") installieren
library(prada) Oder so:
source("https://raw.githubusercontent.com/sebastiansauer/prada/master/R/NAME_bayesbox.R")Unsere Informationen sind:
p_Erde <- .5
p_Bath42 <- .5
Lik_Erde <- dbinom(x = k, size = n, prob = wasser_erde)
Lik_Bath42 <- dbinom(x = k, size = n, prob = wasser_bath42)bb <- bayesbox(hyps = c("Erde", "Bath42"),
priors = 1,
liks = c(Lik_Erde, Lik_Bath42),
round = 2)
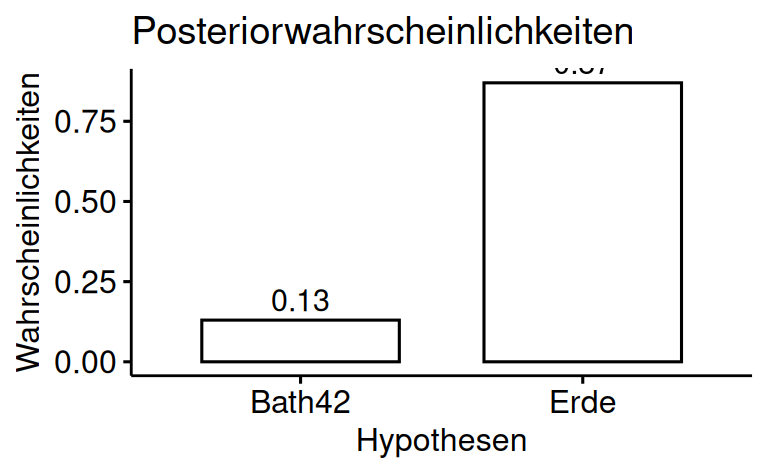
bb| hyps | priors | liks | post_unstand | post_std |
|---|---|---|---|---|
| Erde | 1 | 0.27 | 0.27 | 0.87 |
| Bath42 | 1 | 0.04 | 0.04 | 0.13 |
Falsch. Die Daten sprechen eher für die Erde.
Answerlist
- Falsch
- Wahr
Categories:
- quiz
- probability
- bayes
- num