r <- .99 # Reißfestigkeit des einfaches Seils
R10 <- r^10 %>% round(2) # Reißfestigkeit des 10-fachen Seilsalphafehler-inflation3
Aufgabe
Eine Klettererin verwendet ein Seil, dass eine Sicherheit von \(r=.99\) hat: mit einer Wahrscheinlichkeit von 1% reißt das Seil. Jetzt knüpft sie mehrere dieser Seile (hintereinander, Seil an Seil) zusammen zu einem “Gesamtseil”. Wie groß ist die Gefahr, dass das „Gesamtseil“ reist?
Hinweise:
- Etwaige (physikalisch plausible) Verringerung der Zugfestigkeit durch (Seilbiegung aufgrund der) Knoten ist zu vernachlässigen.
- Sie knüpft 10 Seile zusammen.
- Beachten Sie die sonstigen Hinweise auf dem Datenwerk.
- Unterstellen Sie Unabhängkeit der einzelnen Ereignisse.
Lösung
Sei \(R\) die Wahrscheinlichkeit, dass das Gesamtseil hält (nicht reißt). \(1-R\) ist dann die Wahrscheinlichkeit des Gegenereignisses: das Gesamtseil reißt.
Allgemein ist \(R\) bei \(k\) Tests (Seilen) gleich \(r\) hoch \(k\): \(R=r^k\). (Das Aufaddieren der Fehlalarm-Wahrscheinlichkeit bezeichnet man als Alphafehler-Inflation.)
Die Gesamtsicherheit lauten also:
R10[1] 0.9Die Antwort (solution) ist aber \(1-R\):
solution <- 1-R10
solution[1] 0.1Vertiefung
Betrachten wir abschließend aus Neugier die Wahrscheinlichkeit, dass die Klettererin abstürzt (\(1-R\)) als Funktion der Anzahl der Seie.
Diese Überlegung ist etwas weiterführender und nicht ganz so zentral, aber ziemlich interessant.
Definieren wir die Parameter:
anz_seile <- 1:20 # von 1 bis max 20 Seile
r <- c(.9, .95, .99, .999) # verschiedene Seil-SicherheitenJetzt erstellen wir einen Tabelle, die alle anz_seile * r Werte kombiniert:
d <-
expand_grid(anz_seile, r)
head(d)| anz_seile | r |
|---|---|
| 1 | 0.900 |
| 1 | 0.950 |
| 1 | 0.990 |
| 1 | 0.999 |
| 2 | 0.900 |
| 2 | 0.950 |
Jetzt berechnen wir für jede Kombination die Gesamtsicherheit R sowie die Wahrscheinlichkeit, dass das Seil reißt, \(1-R\):
d <-
d %>%
mutate(R = r^anz_seile,
seil_reisst_prob = 1 - R)plotten das Ganze mit dem Paket ggpubr:
library(ggpubr)
d <-
d |>
mutate(r_fctr = factor(r)) # um "r" zum Gruppieren zu verwenden, sollte es eine nominale Variable sein, daher wandeln wir mit "factor" in eine nominale Variable um.
ggline(d,
x = "anz_seile",
y = "seil_reisst_prob",
color = "r_fctr",
linetype = "r_fctr",
group = "r_fctr") +
labs(color = "Reißfestigkeit",
linetype = "Reißfestigkeit")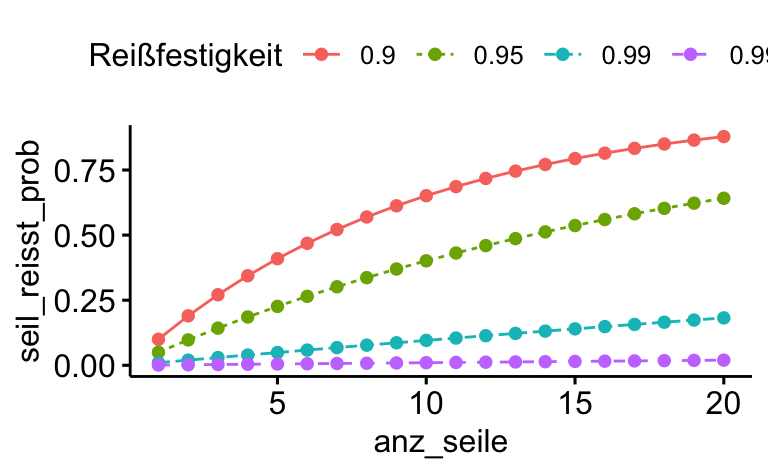
Oder mit ggplot plotten:
d %>%
ggplot(aes(x = anz_seile,
y = seil_reisst_prob,
color = factor(r))) +
geom_line() +
labs(color = "Reißfestigkeit")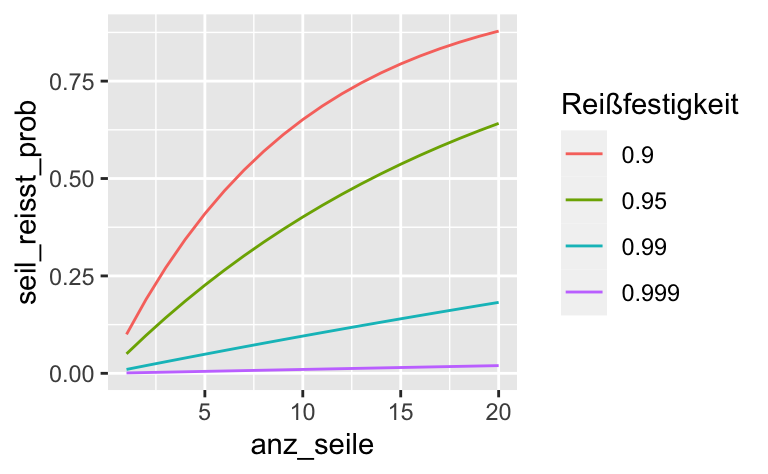
Hat ein Seil eine Sicherheit von 90%, dann will man nicht dranhängen, wenn 20 Seile zusammengeknotet sind!
Die Antwort lautet:
- \(R_{10}= 1-r^{10} = 1 - 0.9 = 0.1\)
Categories:
- probability
- R
- inference
- num