adjustieren2a

regression
2023
string
Published

November 8, 2023

Aufgabe

Betrachten Sie folgendes Modell, das den Zusammenhang des Preises (price) und dem Gewicht (carat) von Diamanten untersucht (Datensatz diamonds).

library(tidyverse)
library(easystats)
diamonds <- read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/ggplot2/diamonds.csv")

Aber zuerst zentrieren wir den metrischen Prädiktor carat, um den Achsenabschnitt besser interpretieren zu können.

diamonds <-
  diamonds %>% 
  mutate(carat_z = carat - mean(carat, na.rm = TRUE))

Dann berechnen wir ein (nicht-bayesianisches, sondern frequentistisches) Regressionsmodell:

lm1 <- lm(price ~ carat_z, data = diamonds)
parameters(lm1)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 3932.800 6.667655 0.95 3919.731 3945.868 589.8325 53938 0
carat_z 7756.426 14.066579 0.95 7728.855 7783.996 551.4081 53938 0

Zur Verdeutlichung ein Diagramm zum Modell:

estimate_relation(lm1) |> plot()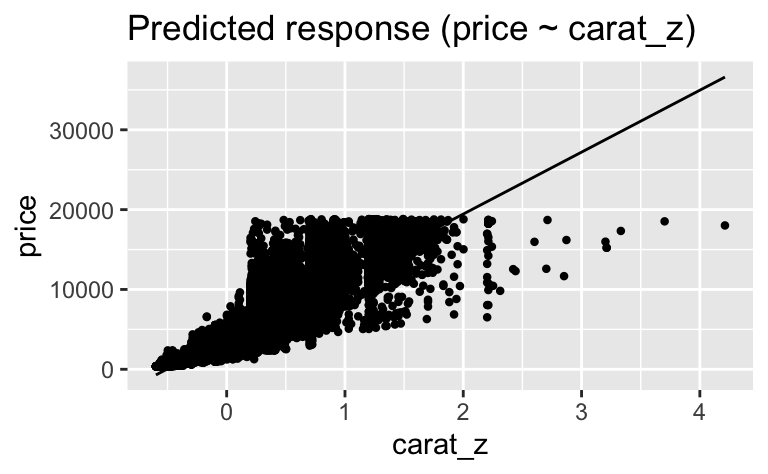

Aufgaben:

  1. Was kostet in Diamant mittlerer Größe laut Modell lm1? Runden Sie auf eine Dezimale. Geben Sie nur eine Zahl ein.

  2. Geben Sie eine Regressionsformel an, die lm1 ergänzt, so dass die Schliffart (cut) des Diamanten kontrolliert (adjustiert) wird. Anders gesagt: Das Modell soll die mittleren Preise für jede der fünf Schliffarten angeben. Geben Sie nur die Regressionsformel an. Lassen Sie zwischen Termen jeweils ein Leerzeichen Abstand.

Hinweis: Es gibt (laut Datensatz) folgende Schliffarten (und zwar in der folgenden Reihenfolge):

diamonds %>% 
  distinct(cut)
cut
Ideal
Premium
Good
Very Good
Fair











Lösung

  1. Unser Modell lm1 schätzt den Preis eines Diamanten mittlerer Größe auf etwa 3932.5 (was immer auch die Einheiten sind, Dollar vermutlich). Da der Prädiktor carat_z zentriert ist, entspricht ein Wert von 0 dem Mittelwert der ursprünglichen Verteilung, carat. Der Y-Wert, wenn X=0, wird vom Intercept angegeben.
parameters(lm1)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 3932.800 6.667655 0.95 3919.731 3945.868 589.8325 53938 0
carat_z 7756.426 14.066579 0.95 7728.855 7783.996 551.4081 53938 0

Oder so:

coef(lm1)
(Intercept)     carat_z 
   3932.800    7756.426

Alternativ können wir uns mit predict für jeden beliebigen Wert des Prädiktors die Vorhersage des Modells ausgeben lassen.

Wir definieren eine (hier sehr kurze) Tabelle mit Prädiktorwerten, für die wir die Vorhersage laut lm1 wissen möchten:

neue_daten <-
  tibble(carat_z = 0)

Dann weisen wir unseren Lieblingsroboter an, auf Basis von lm1 eine Vorhersage (prediction) für neue_daten zu erstellen.

predict(lm1, newdata = neue_daten)
     1 
3932.8
  1. price ~ carat_z + cut

Dieses zweite Modell könnten wir so berechnen:

lm2 <- lm(price ~ carat_z + cut, data = diamonds)
parameters(lm2)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 2405.180 37.82838 0.95 2331.036 2479.324 63.58136 53934 0
carat_z 7871.082 13.97963 0.95 7843.682 7898.482 563.03950 53934 0
cutGood 1120.332 43.49923 0.95 1035.073 1205.591 25.75521 53934 0
cutIdeal 1800.924 39.34443 0.95 1723.809 1878.039 45.77329 53934 0
cutPremium 1439.077 39.86533 0.95 1360.941 1517.214 36.09846 53934 0
cutVery Good 1510.135 40.24008 0.95 1431.265 1589.006 37.52814 53934 0

Man könnte hier noch einen Interaktionseffekt ergänzen, wenn man Grund zur Annahme hat, dass es einen gibt.

Categories:

  • regression
  • ‘2023’
  • string