Verteilungen-Quiz-05

distributions

probability

bayes

paper

Verteilungen-Quiz

Verteilungen-Quiz24

qm2-pruefung2023

Published

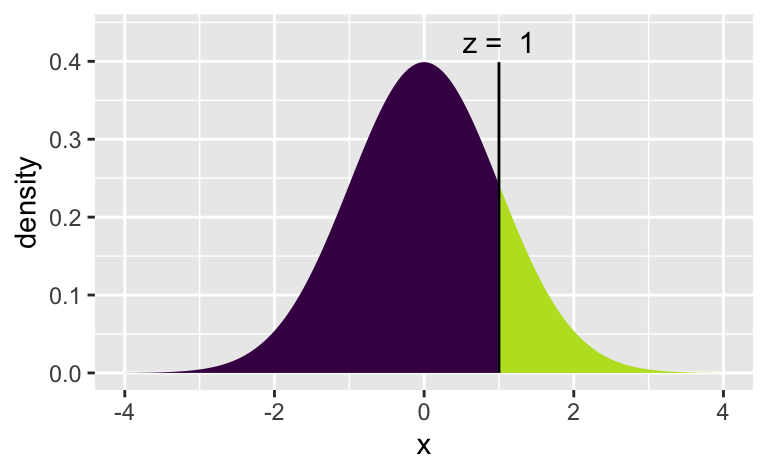
November 20, 2022

Exercise

Ist folgende Aussage wahr?

Ist eine stetige Verteilung symmetrisch, dann gilt

\(Pr(X \ge \bar{x} + 1) = Pr(X \le \bar{x} - 1)\).

Answerlist

Ja
Nein

Solution

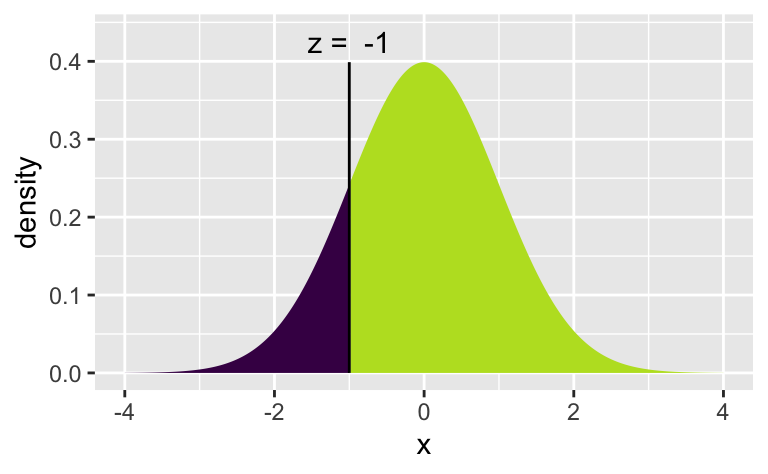
Betrachten wir eine stetige symmetrischer Verteilung und “schneiden” einmal bei \(x=-1\) und einmal bei \(x=1\) ab:

[1] 0.8413447

[1] 0.1586553

In beiden Fällen schneiden wir “nach außen hin” gleich viel Masse ab.

Die Aussage ist also

Wahr

Categories:

distributions
Verteilungen-Quiz
probability
bayes
simulation

---
exname: Verteilungen-Quiz-05
extype: schoice
exsolution: 10
exshuffle: no
categories:
- distributions
- probability
- bayes
- paper
- Verteilungen-Quiz
- Verteilungen-Quiz24
- qm2-pruefung2023
date: '2022-11-20'
slug: Verteilungen-Quiz-05
title: Verteilungen-Quiz-05

---





```{r global-knitr-options, include=FALSE}
knitr::opts_chunk$set(fig.pos = 'H',
                      fig.asp = 0.618,
                      fig.width = 4,
                      fig.cap = "", 
                      fig.path = "",
                      echo = TRUE,
                      message = FALSE,
                      fig.show = "hold")



```






# Exercise

Ist folgende Aussage wahr?

Ist eine stetige Verteilung symmetrisch,  dann gilt

$Pr(X \ge \bar{x} + 1) = Pr(X \le \bar{x} - 1)$.


Answerlist
----------
* Ja
* Nein



</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>

# Solution

Betrachten wir eine stetige symmetrischer Verteilung
und "schneiden" einmal bei $x=-1$ und einmal bei $x=1$ ab:

```{r echo = FALSE, fig.show = "hold"}
mosaic::xpnorm(1, 0, 1)
mosaic::xpnorm(-1, 0, 1)
```


In beiden Fällen schneiden wir "nach außen hin" gleich viel Masse ab.




Die Aussage ist also


* Wahr





---

Categories: 

- distributions
- Verteilungen-Quiz
- probability
- bayes
- simulation