set.seed(42)
p_grid <- seq(from = 0, to = 1, length.out = 1000)
prior <- case_when(
p_grid < 0.5 ~ 0,
p_grid >= 0.5 ~ 1)
likelihood <- dbinom(8, size = 15, prob = p_grid)
unstand_posterior <- likelihood * prior
posterior <- unstand_posterior / sum(unstand_posterior)ReThink3m5
Aufgabe
Nehmen wir an, wir haben 8 (Wasser-)“Treffer” (\(W=8\)) bei 15 Würfen (\(N=15\)) erhalten (wieder im Globusversuch).
Nehmen Sie dieses Mal keine gleichverteilte Priori-Verteilung an. Stattdessen verwenden Sie einen Priori-Wert von Null solange \(p < 0.5\) und einen konstanten Wert für \(p \ge 0.5\). Diese Priori-Verteilung kodiert die Information, dass mindestens die Hälfte der Erdoberfläche mit Sicherheit aus Wasser besteht.
Für alle folgenden Berechnungen, vergleichen Sie Ihre Ergebnisse zu der analogen Analyse mit einem konstanten (gleichverteilten) Priori-Wert!
Berechnen Sie die Posteriori-Verteilung und visualisieren Sie sie. Nutzen Sie die Gittermethode.
Ziehen Sie \(10^4\) Stichproben aus der Posteriori-Verteilung, die Sie mit der Gittermethode erhalten haben. Berechnen Sie auf dieser Grundlage das 90%-HDI.
Berechnen Sie die PPV für dieses Modell. Was ist die Wahrscheinlichkeit 8 von 15 Treffer zu erzielen laut dieser PPV?
Auf Basis der aktuellen Posteriori-Wahrscheinlichkeit: Was ist die Wahrscheinlichkeit für 6 Wasser bei 9 Würfen?
Hinweise:
- Berechnen Sie eine Bayes-Box (Gittermethode).
- Verwenden Sie 1000 Gitterwerte.
- Fixieren Sie die Zufallszahlen mit dem Startwert 42, d.h.
set.seed(42). - Gehen Sie von einem gleichverteilten Prior aus.
Quelle: McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.
Lösung
- Berechnen Sie die Posteriori-Verteilung und visualisieren Sie sie. Nutzen Sie die Gittermethode.
tibble(p = p_grid,
posterior = posterior) %>%
ggplot(aes(x = p, y = posterior)) +
# geom_point() +
geom_line() +
labs(x = "Proportion Water (p)", y = "Posterior Density")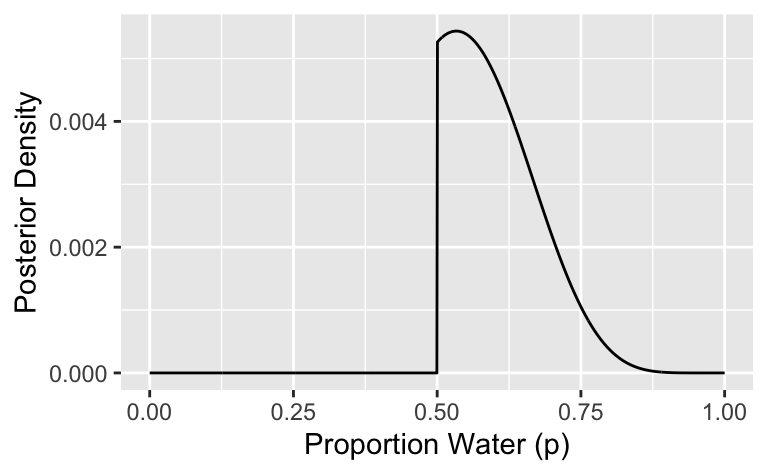
Alternativ können Sie mit ggpubr::ggline() visualisieren.
- Ziehen Sie \(10^4\) Stichproben aus der Posteriori-Verteilung, die Sie mit der Gittermethode erhalten haben. Berechnen Sie auf dieser Grundlage das 90%-HDI.
library(easystats)
# Stichproben (samples) aus der Posteriori-Verteilung:
samples <- sample(p_grid, prob = posterior, size = 1e4, replace = TRUE)
hdi(samples, prob = 0.9)| CI | CI_low | CI_high |
|---|---|---|
| 0.95 | 0.5005005 | 0.7467467 |
- Berechnen Sie die PPV für dieses Modell. Was ist die Wahrscheinlichkeit 8 von 15 Treffer zu erzielen laut dieser PPV?
PPV <-
tibble(w = rbinom(1e4, size = 15, prob = samples)) # w wie Wasser
PPV %>%
count(w == 8) %>%
mutate(prop = n/sum(n))| w == 8 | n | prop |
|---|---|---|
| FALSE | 8508 | 0.8508 |
| TRUE | 1492 | 0.1492 |
- Auf Basis der aktuellen Posteriori-Wahrscheinlichkeit: Was ist die Wahrscheinlichkeit für 6 Wasser bei 9 Würfen?
PPV <-
PPV %>%
mutate(w2 = rbinom(1e4, size = 9, prob = samples))
PPV %>%
count(w2 == 6) %>%
mutate(prop = n/sum(n))| w2 == 6 | n | prop |
|---|---|---|
| FALSE | 7738 | 0.7738 |
| TRUE | 2262 | 0.2262 |
Categories:
- bayes
- ppv
- probability
- string