library(tidyverse)rethink3m2
bayes
post
probability
computer
Exercise
Nehmen wir an, wir haben 8 (Wasser-)“Treffer” (\(W=8\)) bei 15 Würfen (\(N=15\)) erhalten (wieder im Globusversuch).
Ziehen Sie \(10^4\) Stichproben aus der Posteriori-Verteilung basierend auf der Bayesbox-Methode. Gehen Sie von einer gleichverteilung Priori-Wahrscheinlichkeit aus.
Visualisieren Sie die Verteilung der Stichproben.
Berechnen Sie ds 90%-HDI.
Hinweise:
- Berechnen Sie eine Bayes-Box (Gittermethode).
- Verwenden Sie 1000 Gitterwerte.
- Fixieren Sie die Zufallszahlen mit dem Startwert 42, d.h.
set.seed(42). - Gehen Sie von einem gleichverteilten Prior aus.
Quelle: McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.
Solution
Post-Verteilung berechnen:
p_grid <- seq(from = 0, to = 1, length.out = 1000)
prior <- rep(1, 1000)
likelihood <- dbinom(8, size = 15, prob = p_grid)
posterior <- likelihood * prior
posterior <- posterior / sum(posterior)Stichproben-Postverteilung erstellen:
samples <-
tibble(anteil_wasser = sample(p_grid, prob = posterior, size = 1e4, replace = TRUE))
head(samples)| anteil_wasser |
|---|
| 0.4794795 |
| 0.4664665 |
| 0.3863864 |
| 0.4734735 |
| 0.5545546 |
| 0.4404404 |
samples %>%
ggplot() +
aes(x = anteil_wasser) +
geom_histogram() +
labs(title = "Stichproben aus der Posteriori-Verteilung")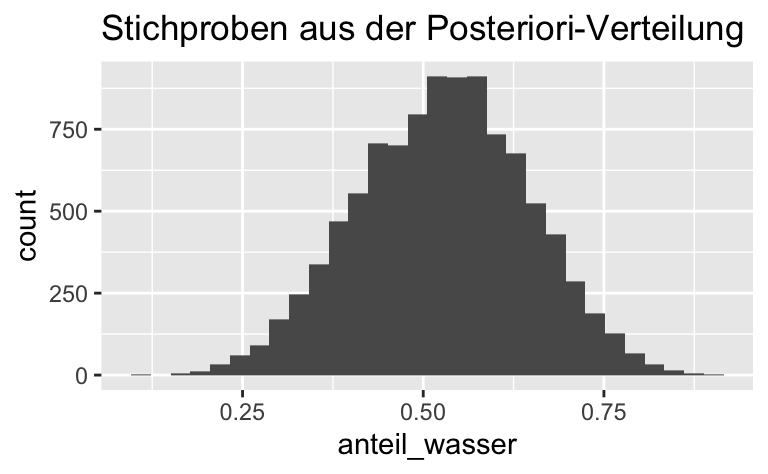
Oder so:
library(ggpubr)
gghistogram(samples, x = "anteil_wasser", bins = 30,
title = "Stichproben aus der Posteriori-Verteilung")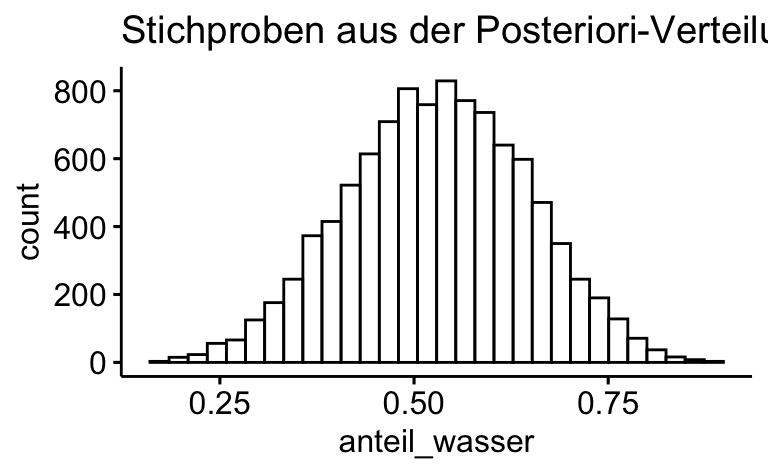
library(easystats)
hdi(samples, prob = 0.9)| Parameter | CI | CI_low | CI_high |
|---|---|---|---|
| anteil_wasser | 0.95 | 0.3033033 | 0.7627628 |
Categories:
- bayes
- post
- probability