p_grid <- seq(from = 0, to = 1, length.out = 100)
prior <- rep(1, 100)
likelihood <- dbinom(8, size = 15, prob = p_grid)
post_unstand <- likelihood * prior
posterior <- post_unstand / sum(post_unstand)
d <- tibble(p = p_grid, posterior = posterior)rethink3m1
bayes
ppv
probability
string
qm2
qm2-pruefung2023
Aufgabe
Nehmen wir an, wir haben 8 (Wasser-)“Treffer” (\(W=8\)) bei 15 Würfen (\(N=15\)) erhalten (wieder im Globusversuch). Gehen Sie wieder von einer “flachen”, also gleichverteilten, Priori-Verteilung aus.
👉 Aufgabe: Berechnen Sie die Posteriori-Verteilung und visualisieren Sie sie. Nutzen Sie die Gittermethode.
Quelle: McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.
Lösung
Jetzt visualisieren; mit ggplot2:
library(tidyverse)
d %>%
ggplot(aes(x = p, y = posterior)) +
# geom_point() +
geom_line() +
labs(x = "Anteil Wasser (p)", y = "Posterior Density")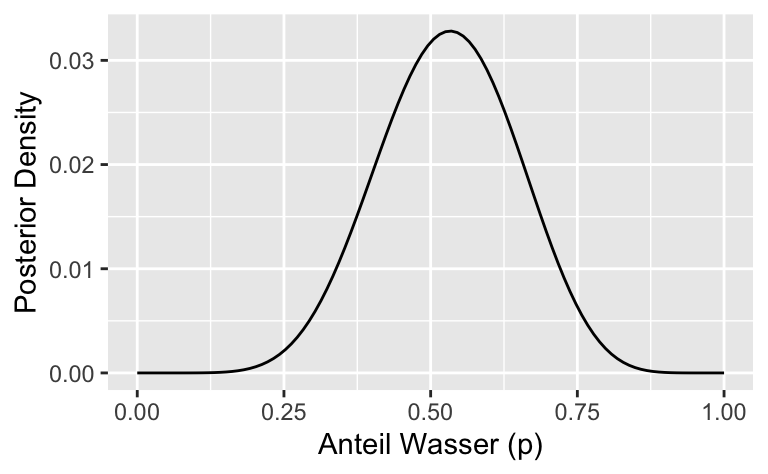
Oder mit ggpubr:
library(ggpubr)
ggline(d, x = "p", y = "posterior",
plot_type = "l")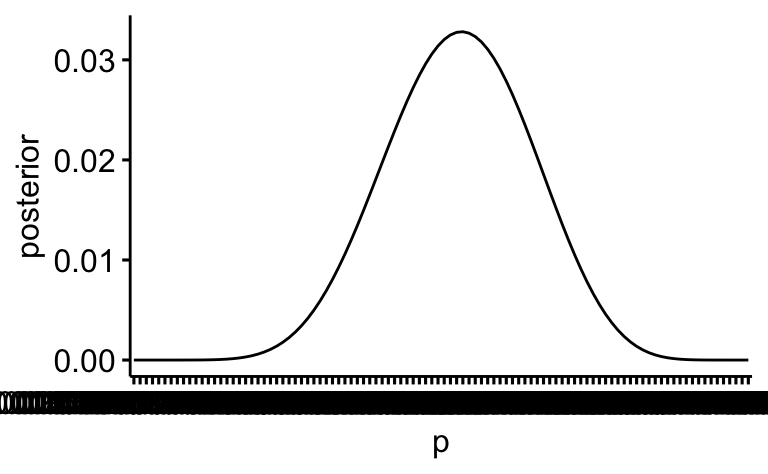
Categories:
- bayes
- ppv
- probability
- string