p_grid <- seq( from=0 , to=1 , length.out=1000 ) # Gitterwerte
prior <- rep( 1 , 1000 ) # Priori-Gewichte
likelihood <- dbinom( 6 , size=9 , prob=p_grid )
unstandardisierte_posterior <- likelihood * prior
posterior <- unstandardisierte_posterior / sum(unstandardisierte_posterior)
# um die Zufallszahlen festzulegen, damit wir alle die gleichen Zahlen bekommen zum Schnluss:
set.seed(42)
# Stichproben ziehen aus der Posteriori-Verteilung
samples <-
tibble(
p = sample( p_grid , prob=posterior, size=1e4, replace=TRUE)) rethink3e1-7
Exercise
Erstellen Sie die Posteriori-Verteilung für den Globusversuch. Nutzen Sie dafür diese Syntax:
Wie viel Wahrscheinlichkeitsmasse liegt unter \(p=0.2\)?
Wie viel Wahrscheinlichkeitsmasse liegt über \(p=0.8\)?
Welcher Anteil der Posteriori-Verteilung liegt zwischen \(p=0.2\) und \(p=0.8\)?
Unter welchem Wasseranteil \(p\) liegen 10% der Posteriori-Verteilung?
Über welchem Wasseranteil \(p\) liegen 10% der Posteriori-Verteilung?
Welches schmälstes Intervall von \(p\) enthält 66% der Posteriori-Wahrscheinlichkeit?
Welcher Wertebereich (synonym: Welches Intervall) von \(p\) enthält 66% der Posteriori-Wahrscheinlichkeit (hier wird Posteriori-Wahrscheinlichkeit synonym gebraucht zu Posteriori-Verteilung)? Wie nennt man diese Arten von Intervall?
Quelle: McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.
Solution
Hier ist eine Visualisierung der Posteriori-Verteilung:
ggdensity(samples, x = "p") # aus "ggpubr"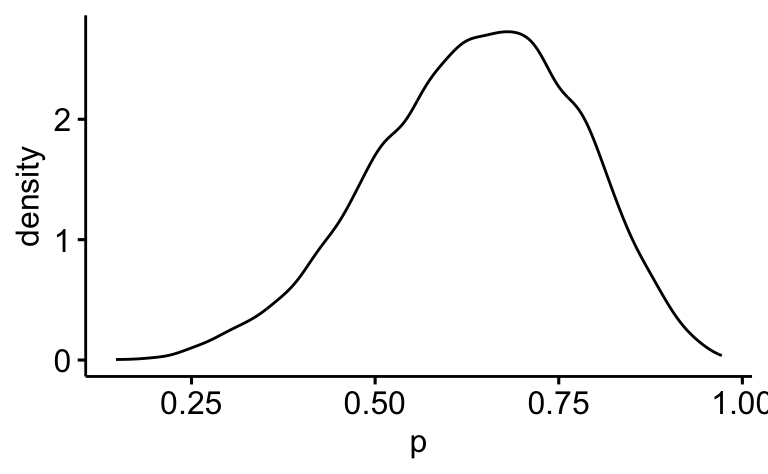
Es finden sich auch Lösungsvorschläge online, z.B. hier
- Wie viel Wahrscheinlichkeitsmasse liegt unter \(p=0.2\)?
samples %>%
count(p < 0.2)| p < 0.2 | n |
|---|---|
| FALSE | 9993 |
| TRUE | 7 |
Fast nix!
- Wie viel Wahrscheinlichkeitsmasse liegt über \(p=0.8\)?
samples %>%
count(p > 0.8)| p > 0.8 | n |
|---|---|
| FALSE | 8842 |
| TRUE | 1158 |
Naja, so gut 10%!
- Welcher Anteil der Posteriori-Verteilung liegt zwischen \(p=0.2\) und \(p=0.8\)?
samples %>%
count(p > 0.2 & p < 0.8) | p > 0.2 & p < 0.8 | n |
|---|---|
| FALSE | 1165 |
| TRUE | 8835 |
Knapp 90%!
- Unter welchem Wasseranteil \(p\) liegen 20% der Posteriori-Verteilung?
Eine Möglichkeit: Wir sortieren \(p\) der Größe nach (aufsteigend), filtern dann so, dass wir nur die ersten 20% der Zeilen behalten und schauen dann, was der größte Wert ist.
samples %>%
arrange(p) %>%
slice_head(prop = 0.2) %>%
summarise(quantil_20 = max(p))| quantil_20 |
|---|
| 0.5165165 |
Andererseits: Das, was wir gerade gemacht haben, nennt man auch ein Quantil berechnen, s. auch hier. Dafür gibt’s fertige Funktionen in R, wie quantile():
samples %>%
summarise(q_20 = quantile(p, 0.2))| q_20 |
|---|
| 0.5165165 |
- Über welchem Wasseranteil \(p\) liegen 10% der Posteriori-Verteilung?
samples %>%
summarise(quantile(p, 0.9))| quantile(p, 0.9) |
|---|
| 0.8098098 |
Mit 90% Wahrscheinlichkeit ist der Wasseranteil höchstens bei 81%.
- Welches schmälstes Intervall von \(p\) enthält 66% der Posteriori-Wahrscheinlichkeit?
library(easystats)
hdi(samples, ci = 0.66)| Parameter | CI | CI_low | CI_high |
|---|---|---|---|
| p | 0.66 | 0.5155155 | 0.7857858 |
- Welcher Wertebereich von \(p\) enthält 66% der Posteriori-Wahrscheinlichkeit (hier wird Posteriori-Wahrscheinlichkeit syonyom gebraucht zu Posteriori-Verteilung)?
Wir nutzen hier die Equal-Tail-Intervall (oder Perzentilintervall genannt), da die Aufgabe keine genauen Angaben macht.
eti(samples, ci = 0.66)| Parameter | CI | CI_low | CI_high |
|---|---|---|---|
| p | 0.66 | 0.5005005 | 0.7747748 |
Ein “mittleres” 2/3-Intervall lässt 1/3 der Wahrscheinlichkeitsmasse außen vor, und zwar gleichmäßig in zwei Hälften links und rechts, also jeweils 1/6 (17%). So ein Intervall heißt Perzentilintervall. Daher synonym:
samples %>%
summarise(PI_66 = quantile(p, prob = c(0.17, .84)))| PI_66 |
|---|
| 0.5005005 |
| 0.7787788 |
Categories:
- bayes
- probability
- post