library(tidyverse)
url_kung <- "https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Howell1.csv"
d <-
read_delim(url_kung, delim = ";") # Strichpunkt als Trennzeichen in der CSV-DateiKung-height
Exercise
Betrachten Sie den Datensatz zur Größe der !Kung:
Untersuchen Sie mit Hilfe eines Diagramms, ob bzw. inwieweit sich die Größe der erwachsenen Personen normalverteilt.
Kennzahlen, die angegeben, inwieweit sich eine Größe normalverteilt, sind Schiefe und Kurtosis. Die Schiefe gibt an, wie symmetrische eine Verteilung ist.
Normalverteilungen sind symmetrisch und haben daher einen Wert von 0 für Schiefe. Kurtosis gibt die “Wölbung”, also wie “spitz” oder “plattgedrückt” eine Verteilung ist. Eine Normalverteilung hat eine Wert von 3 für Kurtosis.
Entsprechende R-Funktionen finden Sie z.B. im Paket moments. Berechnen Sie die beiden Kennzahlen für die Gruppe der Erwachsenen sowie aufgeteilt nach dem Geschlecht. Interpretieren Sie das Ergebnis.
- Diskutieren Sie, inwieweit man aus biologisch fundierten Sachverhalten (also ontologisch) eine Normalverteilung der Körpergröße annehmen kann.
Solution
- Visuelle Prüfung der Normalverteilung
d2 <- d %>%
filter(age >= 18)
d3 <- d2 %>%
select(-male)
ggplot(d2, aes(x = height)) +
geom_density()
ggplot(d2, aes(x = height )) +
facet_wrap(~ male) +
geom_density()
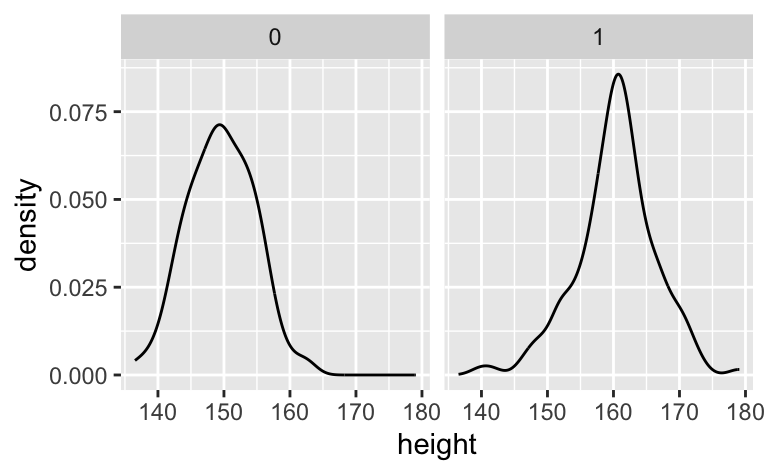
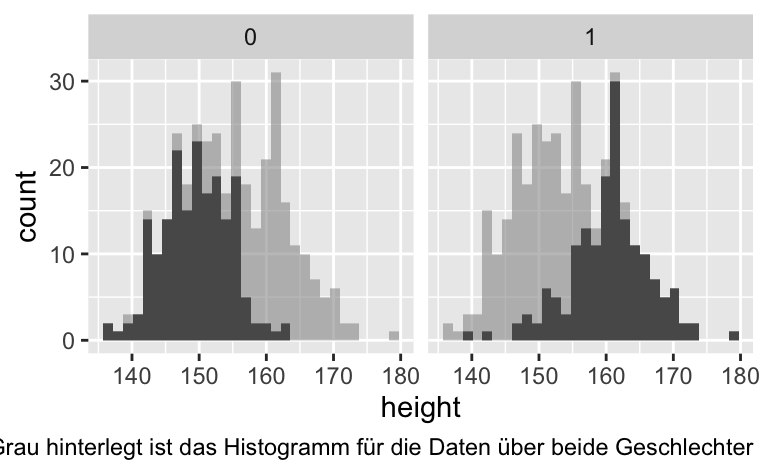
ggplot(d2, aes(x = height)) +
facet_wrap(~ male) +
geom_histogram(data = d3, fill = "grey60", alpha = .6) +
geom_histogram() +
labs(caption = "Grau hinterlegt ist das Histogramm für die Daten über beide Geschlechter")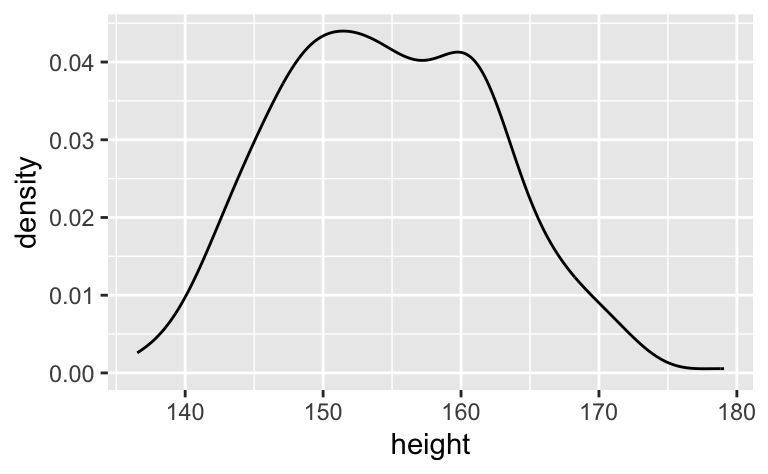
Man kann auch so visualisieren:
library(ggpubr)
d2$male <- as.factor(d2$male)
gghistogram(d2, x = "height", fill = "male")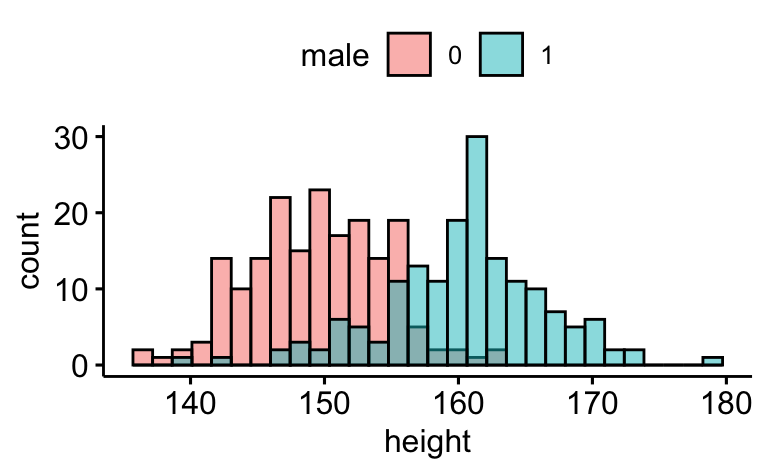
- Schiefe und Kurtosis
library(easystats)
d2 %>% skewness()| Parameter | Skewness | SE | |
|---|---|---|---|
| height | height | 0.1512388 | 0.1294518 |
| weight | weight | 0.1321602 | 0.1294518 |
| age | age | 0.6654057 | 0.1294518 |
| male | male | 0.1257815 | 0.1294518 |
d2 %>% kurtosis()| Parameter | Kurtosis | SE | |
|---|---|---|---|
| height | height | -0.4834334 | 0.2556235 |
| weight | weight | -0.5063574 | 0.2556235 |
| age | age | -0.2128048 | 0.2556235 |
| male | male | -1.9955499 | 0.2556235 |
- Normalverteilung, Begründung
Es ist plausibel anzunehmen, dass der Phänotyp Körpergröße das Resultat des (kausalen) Einflusses vieler Gene ist, vieler Gene, die über einen vergleichbar starken Einfluss verfügen.
Eine besondere Situation stellt das X- bzw. Y-Chromosom dar, das Gene zum Geschlecht bereitstellt. Das Geschlecht ist ein einzelner Faktor, der (erfahrungsgemäß) einen relativ großen Einfluss auf die Körpergröße hat (in Anbetracht, dass vielleicht Tausende Gene additiv die Größe bestimmen). Insofern ist eine klarere Annäherung an die Normalverteilung zu erwarten, wenn man die Geschlechter einzeln betrachtet.
Categories:
- bayes
- ppv
- probability