December 15, 2022





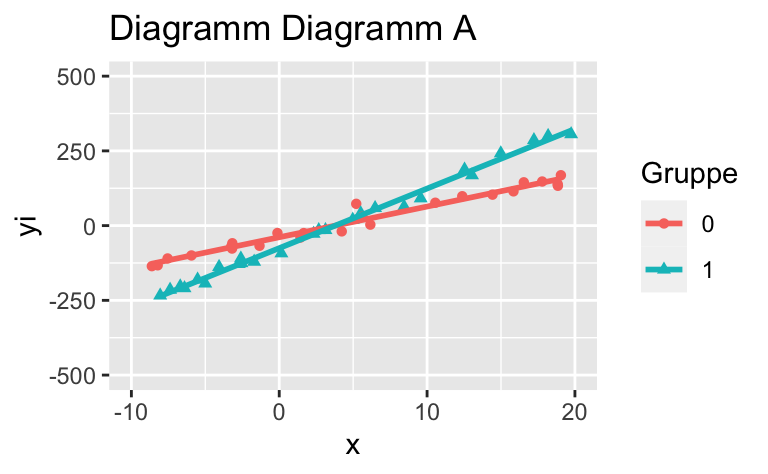
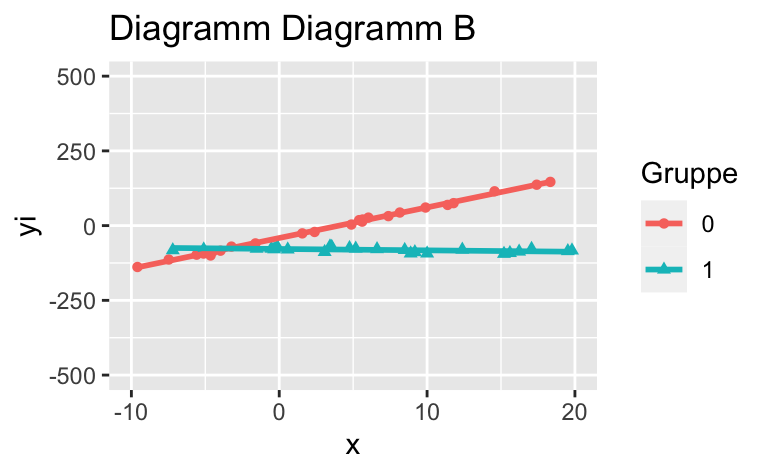
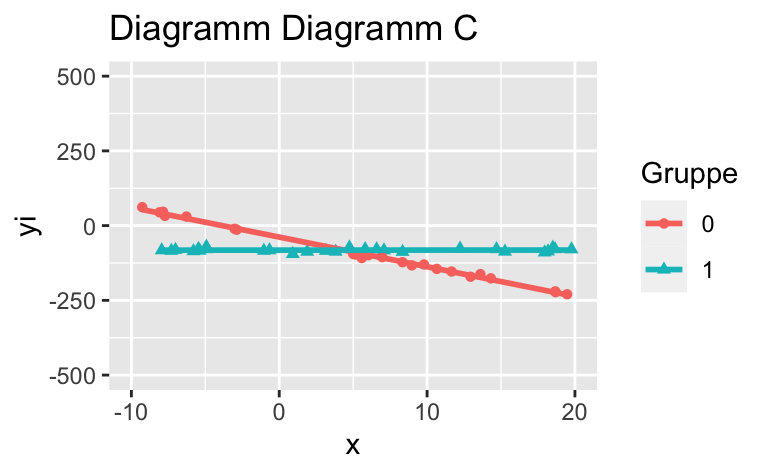
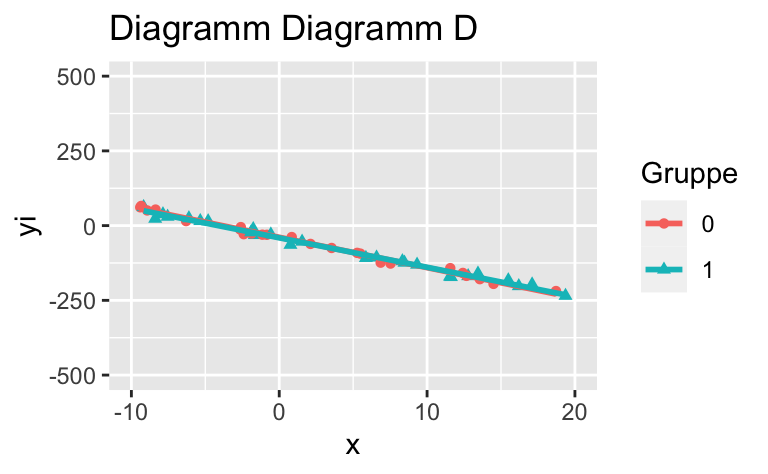
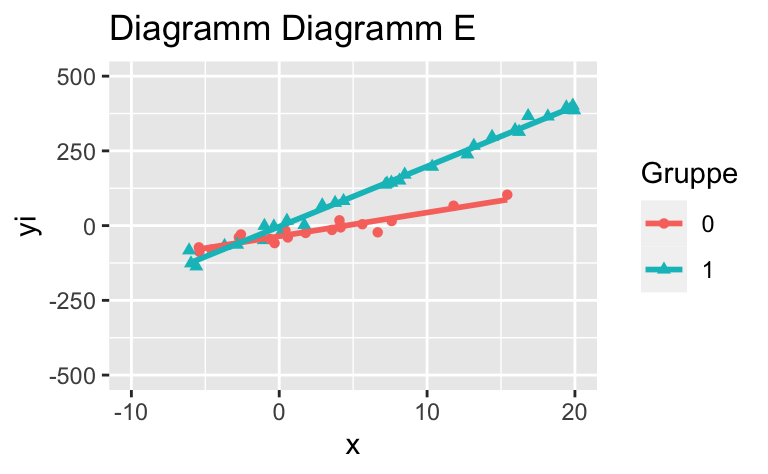
Wählen Sie das Diagramm, in dem kein Interaktionseffekt (in der Population) vorhanden ist (bzw. wählen Sie das Diagramm, dass dies am ehesten darstellt).
Das Streudiagramm Diagramm A zeigt keinen Interaktionseffekt.
Categories:
---
exname: interaktionseffekt1
extype: schoice
exsolution: r mchoice2string(d_five_options_with_sim_data$is_correct, single = TRUE)
exshuffle: no
expoints: 1
exdyn: yes
categories:
- interaction
- regression
- paper
date: '2022-12-15'
title: interaktionseffekt1
---
<!-- based on Karsten Luebke et al. -->
```{r libs, include = FALSE}
library(tidyverse)
library(mosaic)
library(glue)
library(moderndive)
library(knitr)
library(kableExtra)
library(testthat)
library(exams)
```
```{r global-knitr-options, include=FALSE}
knitr::opts_chunk$set(fig.pos = 'H',
fig.asp = 0.618,
fig.width = 4,
fig.cap = "",
fig.path = "",
echo = FALSE,
message=FALSE,
warning = FALSE)
```
# Exercise
```{r defs, echo=FALSE}
# draw random values:
n_set <- c(30, 50, 70)
n <- sample(n_set, 1)
anteil_g1_set <- c(.4, .5, .6)
anteil_g1 <- sample(anteil_g1_set, 1)
n_g1 <- floor(anteil_g1 * n)
xmin_set <- c(-20,-10)
xmin <- sample(xmin_set,1)
xmax_set <- c(10,20)
xmax <- sample(xmax_set,1)
e_set <- c(.1, .2, .3, .4, .5)
e <- sample(e_set, 1)
steigung1_set <- c(-10, 10)
steigung2_set <- c(-40, 0, +40)
achsenabschnitt_set <- c(-40, +40)
interaktion_x_g_set <- c(-10, 0, +10)
```
```{r build-grid, echo = FALSE}
# build grid of all possible combinations
d <-
expand_grid(steigung1_set, steigung2_set, achsenabschnitt_set, interaktion_x_g_set) %>%
mutate(item = glue("$y = {achsenabschnitt_set} + {steigung1_set}\\cdot x + {steigung2_set} \\cdot g + {interaktion_x_g_set} \\cdot xg + \\epsilon$"))
```
```{r comp-dfs, echo = FALSE, comment = ""}
# draw one correct and 4 false answer options:
x <- runif(n, min = xmin, max = xmax)
g <- sample(x = c(0, 1), size = n,
replace = TRUE,
prob = c(anteil_g1, 1-anteil_g1))
# only 5 answer options are supported:
d_four_wrong_options <-
d %>%
filter(interaktion_x_g_set != 0) %>%
sample_n(size = 4) %>%
# choose a "correct" model
mutate(is_correct = FALSE)
# draw one model as "correct" one
d_correct <-
d %>%
filter(interaktion_x_g_set == 0) %>%
sample_n(size = 1) %>%
mutate(is_correct = TRUE)
d_five_options <-
d_four_wrong_options %>%
bind_rows(d_correct)
```
```{r sim-data, echo = FALSE}
# simulate data:
sim_data <- function(steigung1_set,
steigung2_set,
achsenabschnitt_set,
interaktion_x_g_set) {
x <- runif(n, min = xmin, max = xmax)
g <- sample(x = c(0, 1),
size = n,
replace = TRUE,
prob = c(anteil_g1, 1-anteil_g1))
yhat <- achsenabschnitt_set +
steigung1_set * x +
steigung2_set * g +
interaktion_x_g_set * x*g
yi <- yhat + rnorm(n, sd = sd(yhat)*e)
expect_equal(length(yhat), length(yi))
d <-
tibble(x = x,
g = g,
yhat = yhat,
yi = yi)
return(d)
}
get_interaction_sample <- function(d) {
# get interaction effect from lm coefficicents:
mylm <- lm(yi ~ x*g, data = d)
interact_eff <- coef(mylm)["x:g"]
return(interact_eff)
}
d_five_options_with_sim_data <-
d_five_options %>%
mutate(d_sim = pmap(.l = d_five_options %>% select(-c(item, is_correct)),
.f = sim_data)) %>%
mutate(interact_eff_sample = map_dbl(d_sim,
get_interaction_sample)) %>%
sample_n(size = nrow(.)) %>% # shuffle it
mutate(id = glue("Diagramm {LETTERS[1:nrow(.)]}"))
```
```{r plot-scatter, echo = FALSE, comment = "", results = "hide", message = FALSE, fig.show='hold'}
gg_scatter <- function(d_sim, id){
ggplot(data = d_sim) +
aes(y = yi, x = x, color = factor(g), shape = factor(g)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
ggtitle(glue("Diagramm {id}")) +
labs(color = "Gruppe",
shape = "Gruppe") +
scale_x_continuous(limits = c(xmin, xmax)) +
scale_y_continuous(limits = c(-500, + 500))
}
d_five_options_with_sim_data %>%
select(d_sim, id) %>%
pmap(gg_scatter)
```
Wählen Sie das Diagramm, in dem *kein* Interaktionseffekt (in der Population) vorhanden ist (bzw. wählen Sie das Diagramm, dass dies am ehesten darstellt).
```{r questionlist, echo = FALSE, results = "asis"}
answerlist(d_five_options_with_sim_data$id, markup = "markdown")
```
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
# Solution
Das Streudiagramm ``r d_five_options_with_sim_data$id[d_five_options_with_sim_data$is_correct == TRUE]`` zeigt *keinen* Interaktionseffekt.
```{r solutionlist, echo = FALSE, results = "asis"}
answerlist(ifelse(d_five_options_with_sim_data$is_correct, "Wahr", "Falsch"), markup = "markdown")
```
---
Categories:
- interaction
- regression