Bed-Wskt2

probability

bayes

num

qm2

qm2-pruefung2023

Published

November 8, 2023

Aufgabe

Als Bildungsforscher(in) untersuchen Sie den Lernerfolg in einem Statistikkurs.

Eine Gruppe von Studierenden absolviert einen Statistikkurs. Ein Teil lernt gut mit (Ereignis $A$), ein Teil nicht (Ereignis $A^C$). Ein Teil besteht die Prüfung (Ereignis $B$); ein Teil nicht ($B^C$).

(Eselsbrücke: Das Ereignis “A” steht für “Ah, hat Aufgepasst.)

Hinweis: Das Gegenereignis zum Ereignis $A$ wird oft das Komplementärereignis oder kurz Komplement von $A$ genannt und mit $A^C$ bezeichnet.

Wir ziehen zufällig eine/n Studierende/n: Siehe da – Die Person hat bestanden. Yeah!

Aufgabe: Gesucht ist die Wahrscheinlichkeit, dass diese Person gut mitgelernt hat, gegeben der Tatsache, dass dieser Person bestanden hat.

Die Anteile der Gruppen (bzw. Wahrscheinlichkeit des Ereignisses) lassen sich unten stehender Tabelle entnehmen.

row_ids	B	Bneg
A	0.46	0.30
Aneg	0.20	0.04

Hinweise:

Runden Sie auf 2 Dezimalstellen.
Geben Sie Anteile stets in der Form 0.42 an (mit führender Null und Dezimalzeichen).
“Aneg” bezieht sich auf das Komplementärereignis zu A (“A negativ”)
Berücksichtigen Sie die üblichen Hinweise des Datenwerks.

Answerlist

Zeichnen Sie (per Hand) ein Baumdiagramm, um die gemeinsamen Wahrscheinlichkeiten darzustellen. Weiterhin sollen die Randwahrscheinlichkeiten für $A$ dargestellt sein.
Zeichnen Sie (per Hand) ein Baumdiagramm, um diesen Sachverhalt darzustellen.
Geben Sie die Wahrscheinlichkeit des gesuchten Ereignisses an.

Lösung

0.69

A_cond_B <- (AandB / B_marg) %>% round(2)
Aneg_cond_B <- (AnegandB / B_marg) %>% round(2)
A_cond_Bneg <- (AandBneg / Bneg_marg) %>% round(2)
Aneg_cond_Bneg <- (AnegandBneg / Bneg_marg) %>% round(2)

$Pr(A) = 0.76$.

$Pr(B) = 0.656$.

$Pr(AB) = 0.456$.

$Pr(A|B)= 0.7$.

$Pr(\neg A|B) = 0.31$.

$Pr(A|\neg B) = 0.88$.

$Pr(\neg A|\neg B) = 0.12$.

Categories:

probability
conditional
bayes
num

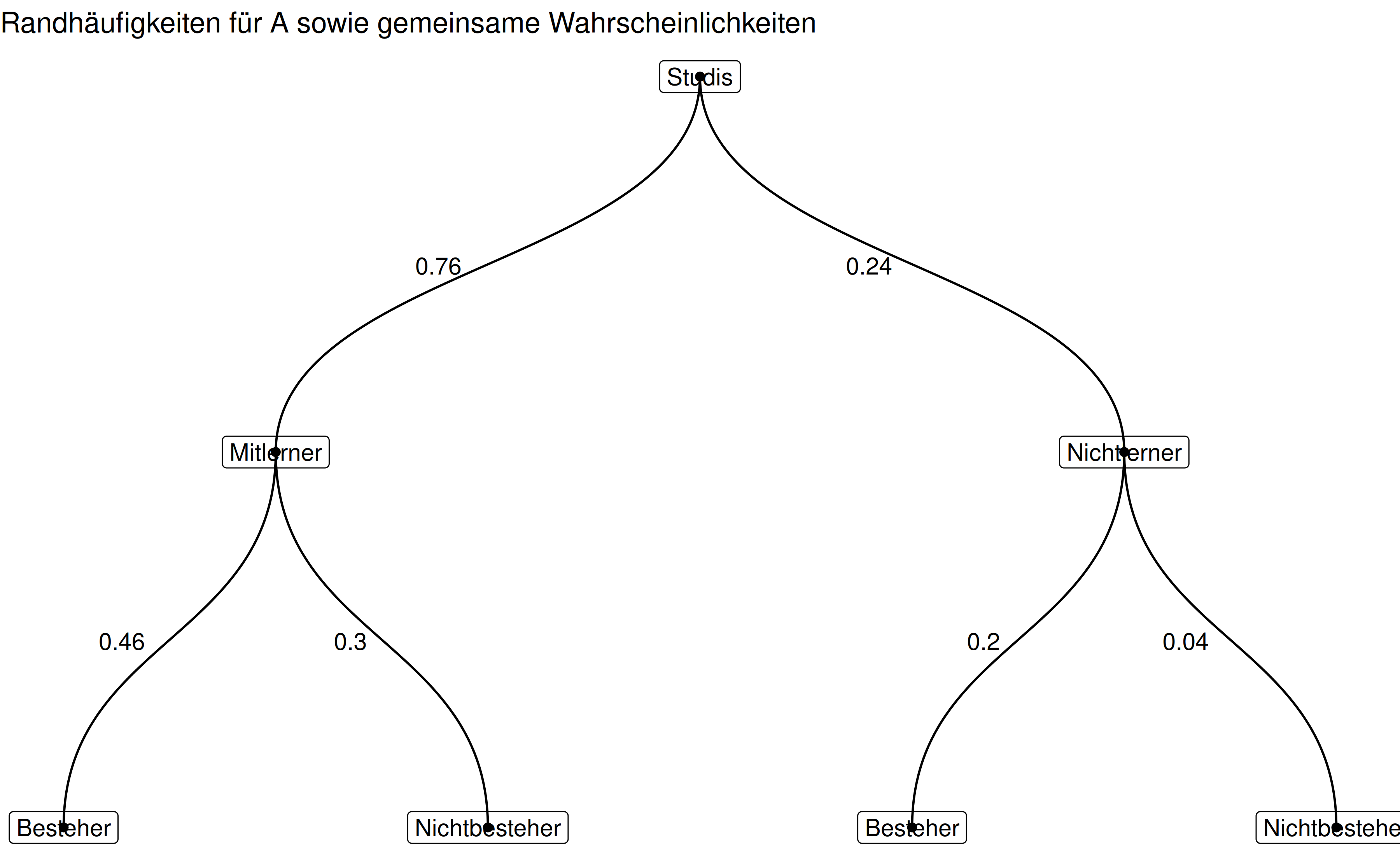
--- exname: Bed-Wskt2 extype: num exsolution: r sol expoints: 1 extol: 0.02 categories: - probability - bayes - num - qm2 - qm2-pruefung2023 date: '2023-11-08' title: Bed-Wskt2 --- ```{r libs, include = FALSE} library(tidyverse) library(glue) library(testthat) library(ggraph) library(igraph) library(gt) ``` ```{r global-knitr-options, include=FALSE} knitr::opts_chunk$set(fig.pos = 'H', fig.asp = 0.618, fig.width = 9, fig.cap = "", fig.path = "", echo = FALSE, message = FALSE, fig.show = "hold", out.width = "50%", dpi = 200) ``` # Aufgabe Als Bildungsforscher(in) untersuchen Sie den Lernerfolg in einem Statistikkurs. ```{r defs} #| echo: false # rbeta(10, 6, 2) A_marg <- rbeta(1, 6, 2) %>% round(2) Aneg_marg <- 1 - A_marg %>% round(2) A_distrib <- rbeta(1, 6, 2) %>% round(2) Aneg_distrib <- rbeta(1, 6, 2) %>% round(2) AandB <- A_marg * A_distrib %>% round(2) AandBneg <- A_marg - AandB %>% round(2) AnegandB <- Aneg_marg * Aneg_distrib %>% round(2) AnegandBneg <- Aneg_marg - AnegandB %>% round(2) B_marg <- AandB + AnegandB %>% round(2) Bneg_marg <- AandBneg + AnegandBneg %>% round(2) d <- tibble( row_ids = c("A", "Aneg", "row_sum"), B = c(AandB, AnegandB, AandB+AnegandB), Bneg = c(AandBneg, AnegandBneg, AandBneg+AnegandBneg) ) %>% mutate(col_sum = B + Bneg) d %>% filter(row_ids == "row_sum") %>% select(B, Bneg) %>% mutate(sum_B_Bneg = sum(B, Bneg)) %>% pull(sum_B_Bneg) %>% expect_equal(1, tolerance = .01) A_cond_B <- AandB / B_marg %>% round(2) Aneg_cond_B <- AnegandB / B_marg %>% round(2) A_cond_Bneg <- AandBneg / Bneg_marg %>% round(2) Aneg_cond_Bneg <- AnegandBneg / Bneg_marg %>% round(2) ``` Eine Gruppe von Studierenden absolviert einen Statistikkurs. Ein Teil lernt gut mit (Ereignis $A$), ein Teil nicht (Ereignis $A^C$). Ein Teil besteht die Prüfung (Ereignis $B$); ein Teil nicht ($B^C$). (Eselsbrücke: Das Ereignis "A" steht für "Ah, hat *A*ufgepasst.) Hinweis: Das Gegenereignis zum Ereignis $A$ wird oft das Komplementärereignis oder kurz Komplement von $A$ genannt und mit $A^C$ bezeichnet. Wir ziehen zufällig eine/n Studierende/n: Siehe da -- Die Person hat bestanden. Yeah! **Aufgabe**: Gesucht ist die Wahrscheinlichkeit, dass *diese Person* gut mitgelernt hat, *gegeben* der Tatsache, dass dieser Person bestanden hat. Die Anteile der Gruppen (bzw. Wahrscheinlichkeit des Ereignisses) lassen sich unten stehender Tabelle entnehmen. ```{r results = "asis"} d %>% select(row_ids, B, Bneg) %>% filter(row_ids != "row_sum") %>% mutate(across(c(B, Bneg), \(x) sprintf(x, fmt = "%.2f"))) %>% gt() ``` *Hinweise*: - Runden Sie auf 2 Dezimalstellen. - Geben Sie Anteile stets in der Form `0.42` an (mit führender Null und Dezimalzeichen). - "Aneg" bezieht sich auf das Komplementärereignis zu A ("A negativ") - Berücksichtigen Sie die üblichen Hinweise des Datenwerks. ```{r} items <- c("Zeichnen Sie (per Hand) ein Baumdiagramm, um die gemeinsamen Wahrscheinlichkeiten darzustellen. Weiterhin sollen die Randwahrscheinlichkeiten für $A$ dargestellt sein.", "Zeichnen Sie (per Hand) ein Baumdiagramm, um diesen Sachverhalt darzustellen.", "Geben Sie die Wahrscheinlichkeit des gesuchten Ereignisses an." ) ``` ```{r questionlist, echo = FALSE, results = "asis"} exams::answerlist(items, markup = "markdown") ``` # Lösung ```{r defs-studis} edf <- #events data frame tibble( from = c("Studis","Studis","Mitlerner", "Mitlerner","Nichtlerner","Nichtlerner"), to = c("Mitlerner","Nichtlerner","Besteher", "Nichtbesteher","Besteher","Nichtbesteher") ) studi_type <- unique(c("Studis","Studis","Mitlerner", "Mitlerner","Nichtlerner","Nichtlerner", "Mitlerner","Nichtlerner","Besteher", "Nichtbesteher","Besteher","Nichtbesteher")) ``` ```{r graph1} studies_props <- round(c(A_marg, 1-A_marg, AandB, AandBneg, AnegandB, AnegandBneg), 2) studis_graph <- tibble( type = unique(c(edf$from, edf$to)) ) studis_graph <- graph_from_data_frame(d = edf, v = studis_graph, directed = TRUE) #V(studis_graph)$name <- studi_type E(studis_graph)$studies_props <- studies_props # as_data_frame(studis_graph, what = "edges") ``` ```{r graph2} studies_prop_cond <- round(c( B_marg, 1-B_marg, A_cond_B, Aneg_cond_B, A_cond_Bneg, Aneg_cond_Bneg ), 2 ) edf2 <- tibble( from = c("Studis", "Studis", "Besteher", "Besteher", "Nichtbesteher", "Nichtbesteher"), to = c("Besteher", "Nichtbesteher", "Lerner", "Nichtlerner", "Lerner", "Nichtlerner") ) studis_graph_v2 <- tibble( type = unique(c(edf2$from, edf2$to)) ) studis_graph2 <- graph_from_data_frame(d = edf2, v = studis_graph_v2, directed = TRUE) E(studis_graph)$studies_props <- studies_props # as_data_frame(studis_graph, what = "edges") E(studis_graph2)$studies_prop_cond <- studies_prop_cond ``` ```{r} sol <- vector(mode = "character", length = 4) ``` A) ```{r fig.align='center'} p1 <- ggraph(studis_graph, layout = 'dendrogram', circular = FALSE) + geom_edge_diagonal(aes(label = studies_props), hjust = 1.5) + geom_node_point() + geom_node_label(aes(label = name)) + theme_void() + labs(title = "Randhäufigkeiten für A sowie gemeinsame Wahrscheinlichkeiten") p1 ``` B) ```{r fig.align='center'} p2 <- ggraph(studis_graph2, layout = 'dendrogram', circular = FALSE) + geom_edge_diagonal(aes(label = studies_prop_cond), hjust = 1.5) + geom_node_point() + geom_node_label(aes(label = name)) + theme_void() + labs(title = "Randhäufigkeiten für B sowie bedingte Wahrscheinlichkeiten") p2 ``` C) ```{r} sol <- A_cond_B %>% round(2) %>% as.character() ``` `r sol` ```{r echo = TRUE} A_cond_B <- (AandB / B_marg) %>% round(2) Aneg_cond_B <- (AnegandB / B_marg) %>% round(2) A_cond_Bneg <- (AandBneg / Bneg_marg) %>% round(2) Aneg_cond_Bneg <- (AnegandBneg / Bneg_marg) %>% round(2) ``` $Pr(A) = `r A_marg`$. $Pr(B) = `r B_marg`$. $Pr(AB) = `r AandB`$. $Pr(A|B)= `r A_cond_B`$. $Pr(\neg A|B) = `r Aneg_cond_B`$. $Pr(A|\neg B) = `r A_cond_Bneg`$. $Pr(\neg A|\neg B) = `r Aneg_cond_Bneg`$. --- Categories: - probability - conditional - bayes - num