| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 146.128218 | 0.95 | 145.2035764 | 147.0433680 | 1 | 0.9999846 | 3704.051 | normal | 154.5971 | 19.355830 |
| weight_c | 0.903986 | 0.95 | 0.8221485 | 0.9891492 | 1 | 0.9997195 | 3764.293 | normal | 0.0000 | 2.997786 |
Bed-Post-Wskt1
Exercise
Beziehen Sie sich auf das Regressionsmodell, für das die Ausgabe mit stan_glm() hier dargestellt ist:
Betrachten Sie folgende Beziehung (Gleichung bzw. Ungleichung):
\[Pr(\text{height}_i = 155|\text{weightcentered}_i=10, \alpha, \beta, \sigma) \quad \Box \quad Pr(\text{height}_i = 160|\text{weightcentered}_i=10, \alpha, \beta, \sigma)\] Die in der obigen Beziehung angegebenen Parameter beziehen sich auf das oben dargestellt Modell.
Ergänzen Sie das korrekte Zeichen in das Rechteck \(\Box\)!
Answerlist
- \(\lt\)
- \(\le\)
- \(\gt\)
- \(\ge\)
- \(=\)
Solution
Als Prädiktorwert (X-Variable) wurde der Achsenabschnitt spezifiziert, also \(x=10\). Der Achsenabschnitt wird mit 146.13 angegeben. Je weiter ein \(y_i\) vom vorhergesagten Wert, \(\hat{y}\) entfernt ist, desto unwahrscheinlicher ist es, gegeben dem Prädiktorwert und dem Modell und den Daten. Für jede Einheit von \(X\) wird \(Y\) größer, also weiter weg von Null.
Der vorhergesagte Wert \(\hat{y}\) lässt sich aus der Tabelle mit den Parameterwerten berechnen:
\(\hat{y} = \beta_0 + x \cdot \beta_1\)
Für das vorliegende Beispiel heißt das:
\(\hat{y} = 146.13 + 10 \cdot 0.9\).
Das Ergebnis ist:
(Intercept)
155.13 Im Detail:
Pakete starten:
Daten importieren:
Daten zentrieren:
Nur Erwachsene:
Modell berechnen:
Paramter des Modells:
| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 146.128218 | 0.95 | 145.2035764 | 147.0433680 | 1 | 0.9999846 | 3704.051 | normal | 154.5971 | 19.355830 |
| weight_c | 0.903986 | 0.95 | 0.8221485 | 0.9891492 | 1 | 0.9997195 | 3764.293 | normal | 0.0000 | 2.997786 |
Modell visualisieren:
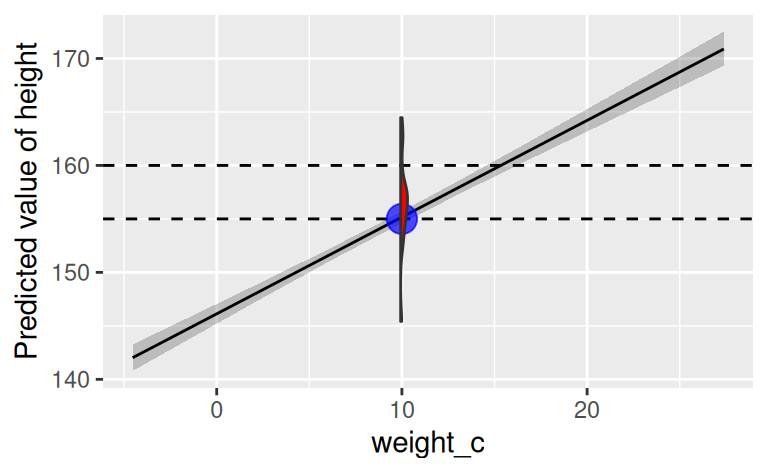
Wie man im Diagramm sieht, ist die Wahrscheinlichkeit bei x = 10 für y=155 größer als für y=160.
Die Wahrscheinlichkeit für einen bestimmten Y-Wert gegeben x = 10` ist auf der Regressionsgeraden am größten (blauer Punkt). Die Punkte auf der Regressionsgeraden sind die vorhergesagten Y-Wert (\(\hat{y}\)) für die gegebenen X-Werte.
Answerlist
- Falsch
- Falsch
- Wahr
- Falsch
- Falsch
Categories:
- regression
- bayes
- post